Световой луч какого цвета самый красивый, по-ваше

ДИФРАКЦИЯ СВЕТА

в узком (наиболее употребительном) смысле — явление огибания лучами света контура непрозрачных тел и, следовательно, проникновение света в область геом. тени; в широком смысле — проявление волновых св-в света в условиях, близких к условиям применимости представлении геометрической оптики.
В естеств. условиях Д. с. обычно наблюдается в виде нерезкой, размытой границы тени предмета, освещаемого удалённым источником. Наиболее контрастна Д. с. в пространств. областях, где плотность потока лучей претерпевает резкое изменение (в области каустической поверхности, фокуса, границы геом. тени и др.). В лабораторных условиях можно выявить структуру света в этих областях, проявляющуюся в чередовании светлых и тёмных (или окрашенных) областей на экране. Иногда эта структура проста, как, напр., при Д. с. на дифракционной решётке, часто очень сложна, напр. в области фокуса линзы. Д. с. на телах с резкими границами используется в инструментальной оптике и, в частности, определяет предел возможностей оптич. устройств.
Первая элем. количеств. теория Д. с. была развита франц. физиком О. Френелем (1816), к-рый объяснил её как результат интерференции вторичных волн (см. ГЮЙГЕНСА — ФРЕНЕЛЯ ПРИНЦИП). Несмотря на недостатки, метод этой теории сохранил своё значение, особенно в расчётах оценочного характера.
Метод состоит в разбиении фронта падающей волны, обрезанного краями экрана, на зоны Френеля.

Рис. 1. Дифракц. кольца при прохождении света: слева — через круглое отверстие, в к-ром укладывается чётное число зон; справа — вокруг круглого экрана.
Считается, что на экране вторичные световые волны не рождаются и световое поле в точке наблюдения определяется суммой вкладов от всех зон. Если отверстие в экране оставляет открытым чётное число зон (рис. 1), то в центре дифракц. картины получается тёмное пятно, при нечётном числе зон — светлое. В центре тени от круглого экрана, закрывающего не слишком большое число зон Френеля, получается светлое пятно. Величины вкладов зон в световое поле в точке наблюдения пропорциональны площадям зон и медленно убывают с ростом номера зоны. Соседние зоны вносят вклады противоположных знаков, т. к. фазы излучаемых ими волн противоположны.
Результаты теории О. Френеля послужили решающим доказательством волновой природы света и дали основу теории зонных пластинок. Различают два вида Д. с.— д и ф р а кц и ю Френеля и дифракцию Фраунгофера в зависимости от соотношения между размерами тела b, на к-ром происходит дифракция, и величиной зоны Френеля ?(zl) (а следовательно, в зависимости от расстояния z до точки наблюдения). Метод Френеля эффективен лишь тогда, когда размер отверстия сравним с размером зоны Френеля: b = ?(zl) (дифракция в сходящихся лучах). В этом случае небольшое число зон, на к-рые разбивается сферич. волна в отверстии, определяет картину Д. с. Если отверстие в экране меньше зоны Френеля (b<-?(zl), дифракции Фраунгофера), как, напр., при очень удалённых от экрана наблюдателя и источника света, то можно пренебречь кривизной фронта волны, считать её плоской и картину дифракции характеризовать угловым распределением интенсивности потока. При этом падающий параллельный пучок света на отверстии становится расходящимся с углом расходимости j = l/b. При освещении щели параллельным монохроматич. пучком света на экране получается ряд тёмных и светлых полос, быстро убывающих по интенсивности. Если свет падает перпендикулярно к плоскости щели, то полосы расположены симметрично относительно центр. полосы (рис. 2), а освещённость меняется вдоль экрана периодически с изменением j, обращаясь в нуль при углах j, для к-рых sinj=ml/b (m=1, 2, 3, . . .).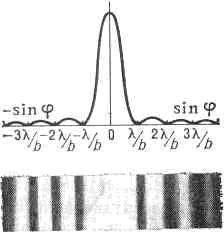

Рис. 2. Дифракция Фраунгофера на щели.
При промежуточных значениях j освещённость достигает макс. значений. Гл. максимум имеет место при m=0 и sinj=0, т. е. j=0. С уменьшением ширины щели центр. светлая полоса расширяется, а при данной ширине щели положение минимумов и максимумов зависит от l, т. е. расстояние между полосами тем больше, чем больше l. Поэтому в случае белого света имеет место совокупность соответствующих картин для разных цветов; гл. максимум будет общим для всех l и представляется в виде белой полоски, переходящей в цветные полосы с чередованием цветов от фиолетового к красному.
В матем. отношении дифракция Фраунгофера проще дифракции Френеля. Идеи Френеля математически воплотил нем. физик Г. Кирхгоф (1882), к-рый развил теорию граничной Д. с., применяемую на практике. Однако в его теории не учитываются векторный характер световых волн и св-ва самого материала экрана. Математически корректная теория Д. с. на телах требует решения сложных граничных задач рассеяния эл.-магн. волн, имеющих решения лишь для частных случаев.
Первое точное решение было получено нем. физиком А. Зоммерфельдом (1894) для дифракции плоской волны на идеально проводящем клине. На больших по сравнению с l расстояниях от острия клина результат Зоммерфельда предсказывает более глубокое проникновение света в область тени, чем это следует из теории Кирхгофа.
Дифракц. явления возникают не только на резких границах тел, но и в протяжённых системах. Такая объёмная Д. с. обусловливается крупномасштабными по сравнению с l неоднородностями диэлектрич. проницаемости среды. В частности, объёмная Д. с. происходит при дифракции света на ультразвуке, в голограммах в турбулентной среде и нелинейных оптич. средах. Часто объёмная Д. с., в отличие от граничной, неотделима от сопутствующих явлений отражения и преломления света. В тех случаях, когда в среде нет резких границ и отражение играет незначит. роль в характере распространения света в среде, для дифракц. процессов применяют асимптотич. методы теории дифференциальных ур-ний. Для таких приближённых методов, к-рые составляют предмет диффузионной теории дифракции, характерно медленное (на размере Я) изменение амплитуды и фазы световой волны вдоль луча.
В нелинейной оптике Д. с. происходит на неоднородностях показателя преломления, к-рые создаются самим распространяющимся через среду излучением. Нестационарный характер этих явлений дополнительно усложняет картину Д. с., в к-рой кроме углового преобразования спектра излучения возникает и частотное преобразование.

Просмотров: 208 | Добавил: binced | Рейтинг: 0.0/0

Всего комментариев: 0

Бесплатный хостинг uCoz